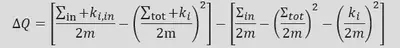社区发现算法——Louvain

社区结构是社交网络的一个重要特征，通常定义为具有紧密联系的一组节点。社区内的节点连接紧密，即内聚性强；社区之间连接较为松散，即耦合度弱。社区发现算法从原理上可分为分离和聚合两类。

Louvain算法：聚合法，是使用优化模块度的方法以提高社区划分效率的方法。 模块度Q：社区内节点的连边数与随机情况下的边数之差。

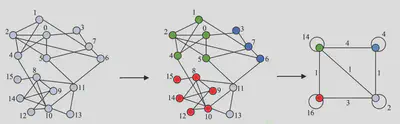
Louvain算法流程： 1.将图中的每个节点看成一个独立的社区，社区的数目与节点的数目相同。 2.对于每个节点i，依次尝试把i分配到其每个邻居节点所在的社区，计算分配前与分配后的模块度增益（∆Q ），并记录∆Q最大的邻居节点；如果max∆Q>0，则把节点i分配到∆Q最大的邻居节点所在的社区，否则保持不变。 3.重复2，直到所有节点的所属社区不再变化。 4.对图进行压缩，将所有在同一个社区的节点压缩成一个新节点，原社区内节点之间的边的权重转化为新节点的权重，原社区间的边权重重转化为新节点间的边权重。如图：

5.重复上述步骤，直到整个图的模块度不发生变化。

Q的计算公式：

其中，A_ij 表示节点i和节点j之间边的权重，k_j 表示所有和节点j连接的边的权重之和，k_i 表示所有和节点i连接的边的权重之和。c_i 表示节点i所属的社区，当节点i和节点j在同一个社区时，δ(c_i,c_j)为0，否则为1。随机情况下，节点i和节点j的期望连接权重为k_i×k_j/2m，A_ij−(k_i k_j)/2m 为节点i和j实际连接权重与期望连接权重之差。

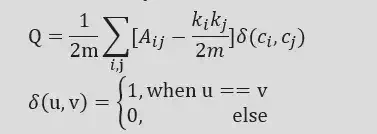
模块增益度∆Q的计算公式：

公式2前半部分表示将节点i加入到社区c后的模块度；后半部分表示加入节点i之前，社区c和节点i作为一个独立社区时，二者的模块度之和。两者相减为模块度的增益。